Statistical intuition fails

Warning: this post contains some mathematics. However, non-technical readers may ignore the equations and focus on the concepts, which are far more important in any case.

I am ashamed to say that my statistical intuition has failed me. I was doing some brainteasers and came across this one here:

In a country in which people only want boys every family continues to have children until they have a boy. If they have a girl, they have another child. If they have a boy, they stop. What is the proportion of boys to girls in the country?

My initial thought was there should be more girls than boys. But this is completely false. As long as all births are independent and a boy or a girl remains equally likely, the ratio of boys to girls in the whole population will be 1 (assuming the population is large). The choice the parents make of when to stop having babies has no influence on the overall distribution of boys or girls. This is actually obvious if you think about it, but you can also prove it mathematically as follows:

Let X₁… X_n be the number of girls in each household in the country. These have a iid geometric distributions and the ratio of boys to girls is

By the law of large numbers this tends to
,
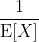which is 1.

In real life, and in financial markets, our statistical intuition also fails us. One of the reasons I think I will never be able to be a trader (or at least not a good one) is that I will never trust any decision I make. It’s only through meticulous analysis, by slowing down, that you can overcome your biases and that is exactly the opposite of trading.