Momentum is an age-old feature of financial
markets. It is perhaps the simplest and also the most puzzling of the “anomalies”
discovered. It is simply the tendency
for assets (for example shares of some company) that did well (or poorly) in
the past to continue to do so for a time in the future. It has been extensively
examined in academia and has been found to be present in virtually all markets
and going as far back as we have data. It has even persisted some decades after
being extensively investigated for the first time. And still, it seems, we do
not understand it very well. In today’s post I just want to highlight some
different momentum strategies and their uses.
A property and a strategy
Momentum is a property of asset prices in markets and momentum strategies try to benefit from this
property. One way of understanding momentum is to consider different momentum
strategies and the profits they make, which gives an indirect means of understanding
how asset prices work. For investors, of course, this is perhaps the most
convenient way to study momentum as they are inherently interested in the
strategies. They only care about momentum as a property if they can exploit it.
The distinction between momentum as a property and as a strategy is not always
clear because academics have not yet, I think, deemed it important to make the
distinction explicit and thus both are simply called momentum.
How to construct a momentum strategy
Momentum strategies come in all shapes and
forms. Basically all of technical analysis is some kind of momentum strategy. A
very general way of thinking about constructing a momentum strategy is depicted
in the picture below. One starts by identifying some kind of trend (or signal)
for each of the assets you are considering. This gives the direction of the
momentum for the asset (for instance up or down). One can then assign a strength
(or score) to this signal, which can be related to the magnitude of the momentum
or the confidence you place in it. Then based on the signal and strength one
makes an allocation decision – you decide how to bet in order (hopefully) to profit.
Time-series and cross-sectional momentum
Momentum strategies come in two main forms
(though they are related). The first is to consider momentum for individual
assets – the tendency for an asset’s price to go up if it went up in the past. Here the signal and strength are evaluated for
assets in isolation. This is time-series momentum.
This form of momentum can be contrasted with cross-sectional momentum, which considers the momentum of assets
relative to each other, e.g. the tendency of one asset to perform better than other
assets if it also did so in the past, for instance. Here the signal and
strength depends on how assets compare to each other.
Time-series momentum (strategy) tends to do
well if an asset’s return is related positively related to its own past
(property), for instance in what is called an AR(1) process:
Thus a higher return in the past predicts a
higher return in the future.
Cross-sectional momentum (strategy) tends
to do well if one asset’s return is negatively
related to the past return of another asset (property), for instance if (numbering
the assets 1 and 2)
This means that a high return on the one
asset predicts a lower return for the other asset in the future.
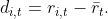
If the asset did better than the average, buy the asset and sell the market and do the opposite if it did worse. This is a bet that assets that had above average performance in the future will continue to do so in the future.
Some simple strategies
Here are some simple strategies, based on a
simple taxonomy:
Signed time-series momentum: buy any asset
that went up in the past; sell any asset that went down.
Signed cross-sectional momentum: this is
analogous to the above, but now invest in deviations from the average return or
the market return. For instance the deviation of asset i’s return from the average
is
If the asset did better than the average, buy the asset and sell the market and do the opposite if it did worse. This is a bet that assets that had above average performance in the future will continue to do so in the future.
Linear time-series strategy: again buy any
asset that went up and sell any asset that went down, but invest more in assets
with larger returns (invest proportionally to the asset’s past return)
Linear cross-sectional strategy: the same
as above, but for deviations from the average (or market) return.
Quantile cross-sectional strategy: buy, for
instance, the top third of assets and sell the bottom third.
In practice only the signed time-series and
quantile cross-sectional strategies are used. The other strategies are,
however, useful in formulating theory. For instance the linear strategies are easier
to cope with mathematically, but amplify volatility too much to make them useful
in practice.
Some references
My
thesis:
- Du Plessis, J. (2013). Demystifying momentum: time-series and cross-sectional momentum, volatility and dispersion. University of Amsterdam. Retrieved from http://www.johandp.com/downloads/johandp_momentum_final.pdf?attredirects=0
Some
empirical articles looking at momentum strategies:
- Jegadeesh, N., & Titman, S. (1993). Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency. The Journal of Finance, 48(1), 65–91. doi:10.1111/j.1540-6261.1993.tb04702.x
- Lewellen, J. (2002). Momentum and Autocorrelation in Stock Returns. (C. H. Schiller, Ed.)Review of Financial Studies, 15(2), 533–564. doi:10.1093/rfs/15.2.533
- Moskowitz, T. J., Ooi, Y. H., & Pedersen, L. H. (2012). Time series momentum. Journal of Financial Economics, 104(2), 228–250. doi:10.1016/j.jfineco.2011.11.003
