This excellent essay, A Mathematician’s Lament, by Paul Lockhart has convinced me of something I suspected since learning actual mathematics at university (and not even, at first, within official lectures): our schooling ruins mathematics for children. The same kind of thinking that has created the education system appears to have infected human resource departments in most major companies. I refer, of course, to the ubiquitous use of aptitude tests (a subset of psychometric assessments). It seems to me that our schools are satisfied with teaching arithmetic rather than mathematics and HR is satisfied with testing “skills” that no candidate will ever need. As with schooling it seems hardly anyone questions the current system. Read more here.
2013/09/23
What do job-application aptitude tests really measure?
It is common practice for companies (including financial companies) to use aptitude tests (mostly numerical and verbal reasoning) in order to assess candidates. I myself have done such tests and though I do not begrudge companies that use them, I have started to question their validity. Do they actually measure something useful? I explore this theme in a blog post on my life-related blog Meditations of Lambchop. Here is an extract from the post
2013/09/03
Don't spot the pattern
If I write 2 then 4 then 6, then we feel good because we know that next comes 8. We can foresee it. We are not in the hands of destiny. Unfortunately, however, this has nothing to do with truth. – Arthur Seldom, The Oxford Murders (movie)
The series 2, 4, 8, could obviously be followed by 16, but also by 10 or 7004.
It's always possible to find a rule, a justification which allows a series to be continued by any number. It all depends on how complicated the rule is. – Arthur Seldom, The Oxford Murders (movie)
I remember getting
questions at school of the form “which number comes next?” At the time I
thought these questions were perfectly normal. I now think they are
nonsensical. As such it troubles me to see similar questions (with diagrams
rather than numbers) are being used in psychometrics assessments. For instance
here are ones called diagrammatic reasoning tests. Whether numbers or diagrams, the
idea is the same and it should be put to an end.
These questions expect you to extrapolate
from a finite set of data. The problem is, as with the above quotes, there are infinitely
many ways to do this. The only difference between them is that some “feel” more
right than others. They are intuitive, they are “simple”. But both of these
things are in fact rather subjective. And so while these questions pretend to have
only one right answer, they really do not.
Here is an example. The series 1 2 3 5 …
This could be “all integers with at most
one factor”, i.e. all the primes and the number 1 – then the next number is 7.
It could also be the Fibonacci sequence, but starting at 1 2 instead of 1 1 –
then the next number is 8. Of course one
could think up infinitely many rules for completing this sequence. Another
simple rule is to assume it is periodic 1 2 3 5 1 2 3 5…. - then the next
number is 1. Of course if you looked only at the first three elements in the
series you would probably guess the next number is 4.
The question, then is not really “what is
the next number?” it is: Find a function from the natural numbers to the
natural numbers which has the given sequence as its first mappings. The function
should be “simple”, meaning it should be described (possibly as a recurrence
relation) only with addition, subtract, exponentiation, etc. and should be the
one function that whoever is marking the question would think is the simplest.
The problem is that the problem is never
actually stated like this. The ways in which you are allowed to describe your function
are not enumerated and there is no objective means of determining what is
“simple”. Thus for any above mediocre mind, the problem is not to find the next number, but to determine how far beyond the standard set of descriptions for functions they should allow their mind to search.
“simple”. Thus for any above mediocre mind, the problem is not to find the next number, but to determine how far beyond the standard set of descriptions for functions they should allow their mind to search.
Thus the question really only does the
following: it forces you to confine your search to what is expected already. It
hinders the ability to think beyond this and it penalises anyone who happens to
think differently from the standard. It creates a false impression of truth and
limits human creativity. The only way to ask these questions (if you have to
ask them at all) is to give a precise description of the form of function
allowed and then make sure only one function in this set satisfies the
requirements. The same is true for diagrammatic questions.
2013/08/28
Stop confusing clever with lucky
I get very annoyed when I see idiotic journalism, such as this article (admittedly Business Insider does not exactly maintain high standards of journalism, but in this case they just copied CNBC). To recap: one 22-year old kid put all his savings into Tesla shares (and later options on Tesla shares) and today has made quite a hefty profit. But when his friends told him he was crazy, they were right.
It is stupid to present this kid’s outstanding luck as success. He was not successful – he was blindly, stupidly, and ignorantly lucky. There was absolutely no way of knowing that Tesla would outshine all the other technology companies. There must be thousands of investors who have similarly bet heavily in some particular stock and found themselves losing everything. I am, of course, not saying anything new here. Taleb argued just these lines in his book Fooled by Randomness, which everyone should read.
But we don’t hear about the investors who lose everything. We only hear about the ones who strike it lucky. Because we think they are special, that they had some special foresight. Mostly they were just lucky.
I admit that markets are not efficient. Some people may have the ability, through research, to increase their chances of doing well. Most active managers think they have this ability (and all of them claim to have it). But only the stupid ones would invest most of their capital in one stock. There is too much room for error.
Warren Buffett is often cited as an example of an investor that managed to beat the market with his foresight, and this may be true (considering his long track record). But he was also very lucky. When he was just starting he invested 75% of his worth in one stock, GEICO, which paid off handsomely. This was after just one conversation with an executive there (one who became CEO shortly afterward). Buffett was extremely lucky. If that single investment had not paid off (and how do you really know it will pay off after speaking to one person, who can’t control the direction of the entire company?) we would never have heard the name Buffett.
Taking stupid risks is fine if you have a safety net (for instance rich parents), because then you’re not really putting all your eggs in one basket. For the rest of us: ignore the media when it tells you people who risked everything were smart. They were lucky.
References
It is stupid to present this kid’s outstanding luck as success. He was not successful – he was blindly, stupidly, and ignorantly lucky. There was absolutely no way of knowing that Tesla would outshine all the other technology companies. There must be thousands of investors who have similarly bet heavily in some particular stock and found themselves losing everything. I am, of course, not saying anything new here. Taleb argued just these lines in his book Fooled by Randomness, which everyone should read.
But we don’t hear about the investors who lose everything. We only hear about the ones who strike it lucky. Because we think they are special, that they had some special foresight. Mostly they were just lucky.
I admit that markets are not efficient. Some people may have the ability, through research, to increase their chances of doing well. Most active managers think they have this ability (and all of them claim to have it). But only the stupid ones would invest most of their capital in one stock. There is too much room for error.
Warren Buffett is often cited as an example of an investor that managed to beat the market with his foresight, and this may be true (considering his long track record). But he was also very lucky. When he was just starting he invested 75% of his worth in one stock, GEICO, which paid off handsomely. This was after just one conversation with an executive there (one who became CEO shortly afterward). Buffett was extremely lucky. If that single investment had not paid off (and how do you really know it will pay off after speaking to one person, who can’t control the direction of the entire company?) we would never have heard the name Buffett.
Taking stupid risks is fine if you have a safety net (for instance rich parents), because then you’re not really putting all your eggs in one basket. For the rest of us: ignore the media when it tells you people who risked everything were smart. They were lucky.
References
- Buffett, W. (2010). Letter to the shareholders of Berkshire Hathaway Inc. October. Retrieved from http://www.berkshirehathaway.com/letters/2010ltr.pdf
- Lebeau, P. (2013). College Student Put His Life Savings Into Tesla, Made A Killing. Business Insider. Retrieved August 28, 2013, from http://www.businessinsider.com/college-student-put-his-life-savings-into-tesla-made-a-killing-2013-8
- Taleb, N. N. (2007). Fooled by Randomness (2nd ed.). Penguin.
2013/08/10
Volatility weighting primer
Volatility weighting is one common means of
attempting to improve the risk profiles of strategies, that is to give them smoother
returns. It consists of taking some asset (or the returns from a strategy) and
dividing the investment you make by the (estimated) future volatility of the
strategy. The goal of this is in fact not reduce the volatility of returns, per
sé, but rather the volatility of volatility. In practice it seems that
volatility weighting does seem to work and gives higher Sharpe ratios (a
measure of the amount of return for every unit of risk taken).
Some
simple maths (skip this bit if you fear maths)
Consider for instance an asset with returns
with (for simplicity) sigma σ and epsilon ε
independent and epsilon ε is mean zero with variance 1. Here σ represents the
volatility of the process. It is predictable (the value for the next period is
known today) but it is random – it changes from period to period. The Sharpe ratio of this strategy is
Notice that this ratio is maximised if
volatility is deterministic, that is if the coefficient of variation of
volatility
is zero. Making volatility deterministic
is, in this case, exactly what volatility weighting does.
It is not clear
which of the above two effects is more important in practice, or if they can
even be separated in any meaningful manner. It is clear, though, that
volatility weighting can work even where the relationship with volatility is
positive (so the second effect is not then the most important). It is also true
that for some strategies, for instance momentum, the relationship with
volatility is often negative and so we can expect the timing effect to play a
role as well.
What
we need for volatility weighting to work
- To be able to forecast volatility. It is typical to model volatility as a predictable process, but in practice we cannot even observe volatility directly. There is, however, some evidence that volatility is sticky, so that one can predict it to some degree.
- We need the portion of returns not depending on volatility not be too large. If this is not the case, then we do not have the multiplicative nature of the return series. It does, however, seem that the effect of this portion of returns is not so large as to completely invalidate the use of volatility weighting.
Why
volatility weighting works
- I have already mentioned that there is an effect of stabilising the volatility and that this creates a more stable returns series. In particular we saw earlier that volatility weighting seems to work by reducing the coefficient of variation of volatility.
- There is, however, another possible effect, volatility timing. If returns are negatively related to volatility then volatility weighting will mean investing less when volatility is high and more when it is low, which intuitively seems to be a good strategy. This won’t work if the conditions in the previous section are not met, though.
Own
volatility or underlying volatility
There are many ways to do volatility
weighting. Here are two that I have looked at:
- Weighting a strategy by its own volatility: you look at some investment strategy and estimate its volatility in some form and then scale how much you invest in the entire strategy.
- Weighting the underlying assets: Here you consider some investment strategy based on a set of assets. Now replace the assets with a set of assets that have been volatility weighted. I call this using normalised returns.
2013/08/05
Momentum strategies
Momentum is an age-old feature of financial
markets. It is perhaps the simplest and also the most puzzling of the “anomalies”
discovered. It is simply the tendency
for assets (for example shares of some company) that did well (or poorly) in
the past to continue to do so for a time in the future. It has been extensively
examined in academia and has been found to be present in virtually all markets
and going as far back as we have data. It has even persisted some decades after
being extensively investigated for the first time. And still, it seems, we do
not understand it very well. In today’s post I just want to highlight some
different momentum strategies and their uses.
A property and a strategy
Momentum is a property of asset prices in markets and momentum strategies try to benefit from this
property. One way of understanding momentum is to consider different momentum
strategies and the profits they make, which gives an indirect means of understanding
how asset prices work. For investors, of course, this is perhaps the most
convenient way to study momentum as they are inherently interested in the
strategies. They only care about momentum as a property if they can exploit it.
The distinction between momentum as a property and as a strategy is not always
clear because academics have not yet, I think, deemed it important to make the
distinction explicit and thus both are simply called momentum.
How to construct a momentum strategy
Momentum strategies come in all shapes and
forms. Basically all of technical analysis is some kind of momentum strategy. A
very general way of thinking about constructing a momentum strategy is depicted
in the picture below. One starts by identifying some kind of trend (or signal)
for each of the assets you are considering. This gives the direction of the
momentum for the asset (for instance up or down). One can then assign a strength
(or score) to this signal, which can be related to the magnitude of the momentum
or the confidence you place in it. Then based on the signal and strength one
makes an allocation decision – you decide how to bet in order (hopefully) to profit.
Time-series and cross-sectional momentum
Momentum strategies come in two main forms
(though they are related). The first is to consider momentum for individual
assets – the tendency for an asset’s price to go up if it went up in the past. Here the signal and strength are evaluated for
assets in isolation. This is time-series momentum.
This form of momentum can be contrasted with cross-sectional momentum, which considers the momentum of assets
relative to each other, e.g. the tendency of one asset to perform better than other
assets if it also did so in the past, for instance. Here the signal and
strength depends on how assets compare to each other.
Time-series momentum (strategy) tends to do
well if an asset’s return is related positively related to its own past
(property), for instance in what is called an AR(1) process:
Thus a higher return in the past predicts a
higher return in the future.
Cross-sectional momentum (strategy) tends
to do well if one asset’s return is negatively
related to the past return of another asset (property), for instance if (numbering
the assets 1 and 2)
This means that a high return on the one
asset predicts a lower return for the other asset in the future.
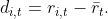
If the asset did better than the average, buy the asset and sell the market and do the opposite if it did worse. This is a bet that assets that had above average performance in the future will continue to do so in the future.
Some simple strategies
Here are some simple strategies, based on a
simple taxonomy:
Signed time-series momentum: buy any asset
that went up in the past; sell any asset that went down.
Signed cross-sectional momentum: this is
analogous to the above, but now invest in deviations from the average return or
the market return. For instance the deviation of asset i’s return from the average
is
If the asset did better than the average, buy the asset and sell the market and do the opposite if it did worse. This is a bet that assets that had above average performance in the future will continue to do so in the future.
Linear time-series strategy: again buy any
asset that went up and sell any asset that went down, but invest more in assets
with larger returns (invest proportionally to the asset’s past return)
Linear cross-sectional strategy: the same
as above, but for deviations from the average (or market) return.
Quantile cross-sectional strategy: buy, for
instance, the top third of assets and sell the bottom third.
In practice only the signed time-series and
quantile cross-sectional strategies are used. The other strategies are,
however, useful in formulating theory. For instance the linear strategies are easier
to cope with mathematically, but amplify volatility too much to make them useful
in practice.
Some references
My
thesis:
- Du Plessis, J. (2013). Demystifying momentum: time-series and cross-sectional momentum, volatility and dispersion. University of Amsterdam. Retrieved from http://www.johandp.com/downloads/johandp_momentum_final.pdf?attredirects=0
Some
empirical articles looking at momentum strategies:
- Jegadeesh, N., & Titman, S. (1993). Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency. The Journal of Finance, 48(1), 65–91. doi:10.1111/j.1540-6261.1993.tb04702.x
- Lewellen, J. (2002). Momentum and Autocorrelation in Stock Returns. (C. H. Schiller, Ed.)Review of Financial Studies, 15(2), 533–564. doi:10.1093/rfs/15.2.533
- Moskowitz, T. J., Ooi, Y. H., & Pedersen, L. H. (2012). Time series momentum. Journal of Financial Economics, 104(2), 228–250. doi:10.1016/j.jfineco.2011.11.003
2013/07/31
Statistical intuition fails
Warning: this post contains some
mathematics. However, non-technical readers may ignore the equations and focus
on the concepts, which are far more important in any case.
I am ashamed to say that my statistical intuition has failed me. I was doing some brainteasers and came across this one here:
In a country in which people only want boys every
family continues to have children until they have a boy. If they have a girl,
they have another child. If they have a boy, they stop. What is the proportion
of boys to girls in the country?
My initial thought was there should be more girls than boys. But this is completely false. As long as all births are independent and a boy or a girl remains equally likely, the ratio of boys to girls in the whole population will be 1 (assuming the population is large). The choice the parents make of when to stop having babies has no influence on the overall distribution of boys or girls. This is actually obvious if you think about it, but you can also prove it mathematically as follows:
My initial thought was there should be more girls than boys. But this is completely false. As long as all births are independent and a boy or a girl remains equally likely, the ratio of boys to girls in the whole population will be 1 (assuming the population is large). The choice the parents make of when to stop having babies has no influence on the overall distribution of boys or girls. This is actually obvious if you think about it, but you can also prove it mathematically as follows:
Let X1… Xn be the number of girls in each household in the country. These have a iid
geometric distributions and the ratio of boys to girls is
By the law of large numbers this tends to
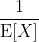 ,
,
which is 1.
which is 1.
2013/07/09
Self-critique
I recently finished my masters thesis and I would now like to do something that most people never do. I am going to
critique my work. I believe that being self-critical is essential not only in
research, but in life in general. In research it is necessary to further the
truth. It is not enough that others are critical of you (though it is
necessary). You must be critical of yourself – only then will you be willing to
remedy your flaws, change your convictions and pursue truth and goodness rather
than your own prejudiced agenda.
I write this post as much to myself as for any reader who
may come across it. It is another public reminder of a lesson I fear I may
forget in the future, and of which I may need to be reminded. Even if you are
not interested in my thesis, some of the points of criticism here may be useful
for your own writing. I found in writing this post that self-criticism is hard.
It’s really hard to come up with anything but weak flaws in your own work. I
reckon it will take time to cultivate a truly self-critical nature.
My thesis was about momentum. I looked at time-series and
cross-sectional momentum and their relationship with volatility and
cross-sectional dispersion, specifically considering volatility weighting as a
means of improving momentum strategies. If this sounds like Greek, do not fear,
for I will be explaining all of this in later posts. Today I just want to list
my critiques, starting with the more serious ones.
Subjective
conclusions drawn from mixed results
I often found when I ran some numbers that I got results
that were not clear-cut for any any one conclusion. Then I had to be
satisfied with making a qualified conclusion if I thought there was enough
support for it in the data. “Enough support” is subjective and others may feel
differently. It may be a wiser course of action not to draw any conclusion at
all, but it may also be far too conservative.
A lack of focus
Good academic research tends to focus on one thing and
examine it thoroughly. My thesis, I think, tried to look at somewhat too much,
and as a result ended up being huge and with not one aspect being treated quite
as it deserved.
Strict assumptions
(that I violate)
In order to prove things easily you need to make
assumptions. Often you end up assuming independence or normality where it is clearly
not the case in the data. In my case I needed to make such assumptions to prove
things about volatility weighting and in at least one case I am not even
certain there is a non-trivial (that is to say, interesting) process that
satisfies my assumptions. I have little choice but to violate my assumptions
(there are for instance no volatility estimators that satisfy the assumptions I had to
make).
Overly detailed
results that are hard to interpret
I have lots and lots and lots of tables in my thesis. They are big and make your eyes sore. Ideally
one should find a way of presenting just the right numbers, without hiding ambiguity
and evidence that doesn’t support your conclusions. It is hard to read text
referring to specific numbers in very large tables and keep track of what is
happening. Making a graph is even better as it gives an immediate impression
(but you may still want to report the numbers so that people can check them). I
had relatively few graphs as I could think of no good way to convert my tables
into something visual. This is a weakness. You may think that academics should
be able to read such dense material, that they should take the time and effort.
It is, however, a simple fact that academics are human and that they do not.
Even if they do, they are less likely to
get the right picture if the information is not presented in accessible manner.
Use of advanced
techniques without necessarily having the appropriate understanding
I used what are called “Robust regressions” in my thesis in
order to cope with the fact that financial data contains so many extreme values.
I had never used robust regressions before and only briefly looked up what the
robust regressions did, then used them. I did not take the time to get well
acquainted with their theory (as this would have been quite a task, I think)
and I simply used a standard weighting function with a standard parameter. Most likely this is still better than simply
using OLS regressions (which I think are absolutely a no-go in financial
research, except as a baseline comparison), but it is still possible that the
version of robust regressions I used were not the most appropriate (deciding what
is appropriate is of course more an art than a science) and it would have been
preferable to have had more training in using them.
Linearity
I used linear models for the theoretical and empirical
investigations. One thing that is clear from finance, though, is that nothing is
linear and so results from linear models can be misleading. We have, however, I
think, only poor substitutes and thus linearity is still common in academia. This
is thus only a weak criticism on my part, but I would like to see a move away
from linear models, if only we could find an accessible and preferably
tractable alternative.
Little thought for
practicalities
I did not consider that I was basing my results on markets
that closed at different times (essentially I assumed they closed at the same
time); I did not include transaction costs, commissions, taxes, etc. This is
not unreasonable. To include all these things meticulously would detract from
the main purpose of the study. But they are important and their inclusion could
potentially change the nature of the relationships found (though this is
unlikely).
If you read my thesis and you think there are other criticisms, then please let me know. Perhaps I'll include them in a further post.
If you read my thesis and you think there are other criticisms, then please let me know. Perhaps I'll include them in a further post.
Labels:
academia,
momentum,
research,
self-criticism,
thesis
2013/03/11
Don't trust research, not even your own
The more
research I do (and I have not done much) the less I trust other research, and
the less I trust my own. When you read a
paper in finance you will invariably find significant results that support the
author’s conclusions. When I run
regressions, my results are weak, sometimes contradicting my hypothesis
sometimes confirming it.
Significance bias
Weak
results don’t get published (and negative results, i.e. results that do not
find evidence for an hypothesis don’t get published either). Academics have an incentive to try things
until they find something significant. Of course, they then only report the
significant results. The problem is firstly that this is a form of data mining
and secondly that there is information in the insignificant results that is now
lost. Future researchers may well duplicate much of the work, not knowing it
has already been tried.
The story bias
We like
stories that fit together. In research (particularly research in finance) this
can be problematic. At some point during your research (or beforehand) you will
develop a theory, a kind of story puts all your results together like pieces of
a puzzle. This will develop long before you have all your results. It’s a good
thing to have a hypothesis before you start running tests on your data – it
helps to avoid data mining. However, the danger is that as you look at your
results, you discount the results that do not fit your story. This may not even be conscious. It’s just the
way your brain works. The danger, then,
is that you only report results that fit your story.
As a
researcher you are likely to have more results at your disposal than you can
reasonably report in an article or thesis. You must condense, summarise, omit. More
than that, you must give the
appearance of a coherent structure, an evidence-based explanation of the
underlying forces you have uncovered. You can’t just say, “well, it’s a bit of
a mess.” Your story has to make sense. But sometimes the world is a mess and
stories don’t work.
Self-examination
I wrote
this post not because I found these tendencies in other researchers. I found
their beginnings in myself. I have careful supervision that will prevent
abuses. In theory peer review should uncover these things as well. In practice,
I don’t trust the peer review system either. Thus this is a public reminder to
myself: be wary of cherry-picking results to suit your prejudices.
2013/01/31
The anonymous referee
In academic articles, you sometimes come across a paragraph
that makes no sense (even on a second or third reading). Very often you will
find, attached to this paragraph, a footnote, which says something like the
following
“We thank the anonymous referee for drawing our attention to this.”
To the anonymous referee, that is exactly what is being
said. But to anyone else reading the article it translates as
“We had to put this in our article in order to get it published because
the anonymous referee is an idiot and insisted on it.”
One can then proceed to read the paper, ignoring that
paragraph. This seems wrong to me. On the one hand I understand the trade-off:
no publication vs make one little, albeit nonsensical, change. I would like to
think I have more honour, more backbone than that, but I probably do not.
I think the anonymous peer review system is flawed. And it
appears I’m not the only that thinks so.
Peer review is currently (at least in some fields and
journals, not all though) double blind. In theory the referee does not know
whose paper they are reviewing and the author does not know who the referee is
(in practice, I think, anonymity is hardly guaranteed, especially in fields
where there are a small number of specialists. Your writing, the references you
choose (especially your own papers) can give you away).
It is one side of this double blindness that bothers me –
that referees are anonymous. The other side may have flaws too, but at least it
should prevent a paper being accepted merely because it is written by a bigshot
academic.
Referee anonymity absolves journals of the responsibility of
explaining their choice of referee (if they choose a referee obviously against
the line of research or too obviously biased for it). It also means referees are
not held accountable for their reviews. They may not take the process seriously
and out of sheer laziness rather than malice block good research or let bad
research pass.
I think that if referees are made known it will allow for greater
dialogue. Referees can be challenged. Their reputations depend on being
thorough. The feedback process may in fact lead to better research.
I think I, like one Dr Bertrand Meyer (see below), will always insist on
signing my reviews (if I am ever in the position to review work for
publication). My reputation is important to me. I want my reviews to reflect on
my reputation (otherwise I will not take them seriously) and I want them to be thorough
and thoughtful (otherwise they will reflect badly on my reputation).
- Meyer, B. (2013). why I sign my referee reports. Retrieved January 29, 2013, from http://se.ethz.ch/~meyer/publications/online/whysign/
- Watson, R. (1985). Anonymous Referees and Blind Refereeing. Proceedings and Addresses of the American Philosophical Association, 85(5), 755–757. Retrieved from http://www.jstor.org/stable/10.2307/3131683
- Wikipedia. (2013). Peer review. Wikipedia. Retrieved January 31, 2013, from http://en.wikipedia.org/wiki/Peer_review
2013/01/28
Review: Models. Behaving. Badly
This book
was written by the famous quant “Emanuel Derman”, whom I mentioned in one of my
blog posts before when I commented on the Financial Modeller’s Manifesto.
I was expecting a lot from this book, I
admit. And I was disappointed. That is not to say that the book did not contain
valuable insight, but I was hoping for more.
Not really about finance: The very long
preamble
If you were
hoping to read a book about finance (or at least financial models) with some
references to other material for diversion (as I was) you will be
disappointed. Most of the book hardly
even mentions finance. Instead it deals with the Emanuel’s (admittedly not
uninteresting) view of models in physics, society (such as during the apartheid era) and
Spinozan philosophy. The point of this, I think, was to illustrate in a more
general setting the idea of a model or a theory. But given that the book is
portrayed as being firstly about “Wall Street” it feels a bit like fluff.
There are
some autobiographical passages about Dermans life in South Africa. I found these
very interesting, but they added little value to the goal of the book. The
point Derman was trying to make (that the models used in apartheid South Africa
failed) could have been made in much less space. But then the book would have been even shorter
than it already is. I hardly think anyone who buys the book would be truly
interested in reading about Spinoza’s theory of emotions (as interesting it
might be philosophically). I certainly hoped the financial stuff would come
soon.
One would
have expected to get at least a good explanation of how models were used during
the financial crisis and how they failed. Instead, the links that Derman makes
with his descriptions of some basic financial models and the financial crisis
are superficial at best. If you want insight into this part of the financial
crisis, you must go elsewhere. Early on
in the book Derman laments what had happened during the crisis and before it: “decline
of manufacturing; the ballooning of the financial sector; that sector’s capture
of the regulatory system; ceaseless stimulus whenever the economy has waivered;
tax-payer-funded bailouts…” It’s a very long list and not one item on it is
treated in the book. We are told that model failure was the cause – we are
never given any more insight than that.
The value of commonsense
I have been
quite critical thus far, but the book does add value. There is a distinction
between models used in physics, which are accurate, and those used in finance
which are, at best, sometimes useful. The latter often treat people as if they
are just particles or objects, which they are not. Derman calls this “pragmamorphism”.
Financial models always leave out something important. The admonition to always
use common sense is valid. However, I was hoping to come away with more insight
than that. Perhaps that’s all there is, really.
Models and theories and facts – Derman does the
unforgivable
Central to
the book is the distinction between “models”, which are based on analogy, and
“theories” which attempt to describe the real world without analogy. Essentially, physics works with theories (mostly) and finance works exclusively with models. This is a useful distinction – though I am not convinced that the two categories are not instead two extremes of a continuum of models. However, as far as thinking about modelling goes, I believe it is very valuable.
“theories” which attempt to describe the real world without analogy. Essentially, physics works with theories (mostly) and finance works exclusively with models. This is a useful distinction – though I am not convinced that the two categories are not instead two extremes of a continuum of models. However, as far as thinking about modelling goes, I believe it is very valuable.
Dr Derman
goes one step further though, doing something I find unforgivable. He claims that a “correct” theory becomes a
fact. Physics models that say there are electrons and that they behave in
certain ways are the truth. I do not
think Dr Derman actually thinks this – because to do so would be to disavow
even the possibility of a theory being overturned, replaced by something
better. And we have seen it done: Newton’s laws, “confirmed” to be accurate for
hundreds of years turned out to be a poor description of reality once you
started looking at things moving near the speed of light.
Physics
uses mathematics and mathematics is not and will never be the real world –
though it is the most useful tool we have for describing the world. In science
(all of science, including physics) we can only ever say this: IF my
model or theory is correct then we would expect certain observations in the
real world.
Science can
never confirm a theory to be correct. Theories that are considered “facts” are
just the ones that have not yet been proven to be wrong. I think that a better
theory than general relativity or quantum electrodynamics may come along – it
may only bring incremental changes or it may bring a revolution in the way we
think about the world. But it is the way we think about the world that changes,
not the world.
Verdict
I must, if
I am kind, conclude that Derman’s book tries to do a little too much (or, if I
am unkind, that it tries to do too little and pads it with fluff): it wants to
be philosophy, biography, essay and social commentary. It does none of these
particularly well.
Reference
Derman,
E., 2012. Models.Behaving.Badly.: Why Confusing Illusion with Reality Can
Lead to Disaster, on Wall Street and in Life, Free Press. Available at:
http://www.amazon.com/Models-Behaving-Badly-Confusing-Illusion-Reality-Disaster/dp/1439164991
[Accessed January 27, 2013].
2013/01/22
Humble academics
(The
following is based on my initial and brief impressions of the quality of
academic writing in finance. I may change my mind later)
I’ve been
reading through (the introductions) of very many articles in finance these past
two weeks. The more I read, the more I realise that in finance the truth is a
very murky prospect. In physics it seems like the truth is more stable
(although physicists have a nasty habit of confusing their “theories” with
reality. They seem to forget when their theories are shown to be wrong that
they ever thought of them as Gospel). But in finance, if you find two papers that
agree, they probably share an author.
I am pretty
sure that all these papers have one thing in common: they are all wrong. But
every author is confident of his conclusions. References to why their results
may be spurious are rare. Hardly ever do authors mention that their underlying
assumptions are completely wrong – it seems standard to just rely on run-of-the-mill
statistical methods, which I cannot believe take into account the wild
randomness of the markets. Very few seem to care.
Academics
in finance needs to be a little more humble. I think every paper should contain
a disclaimer:
“The
results in this paper are only valid under the assumptions of the methods used.
These assumptions are almost certainly violated. The conclusions in this paper
are disputed. Please do not confuse what is presented here with the truth.”
Some tips
for academics:
- Write very clearly the underlying assumptions are – don’t just use methods without being very clear what it is they assume.
- If you’re using a method outside of an area in which it is (proven) valid, write it in CAPS LOCK, because otherwise you’re a fraud, a charlatan.
- Show how the assumptions are violated (note I used “how” not “if”) – not just speculation, I want to see statistical tests and diagrams.
- Please reference everyone who disagrees with you. They’re not right either, but at least we know where to look for alternatives.
- Stop being so sure of yourself.
Readers of
anything in finance (of academic journals, of The Economist, etc.) should
consider that anything can be challenged. There is no absolute truth. If there
is, we cannot discover it, which amounts to the same thing. Live in a state of
scepticism of everything you read. It isn’t fun – but the alternative, as
Voltaire would say, is absurd.
Subscribe to:
Posts (Atom)
